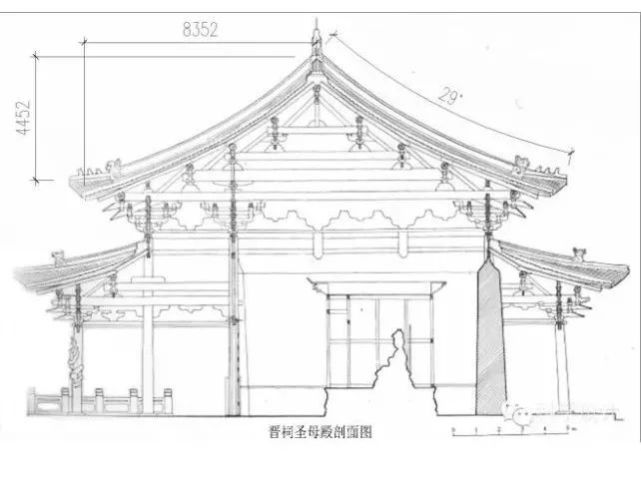
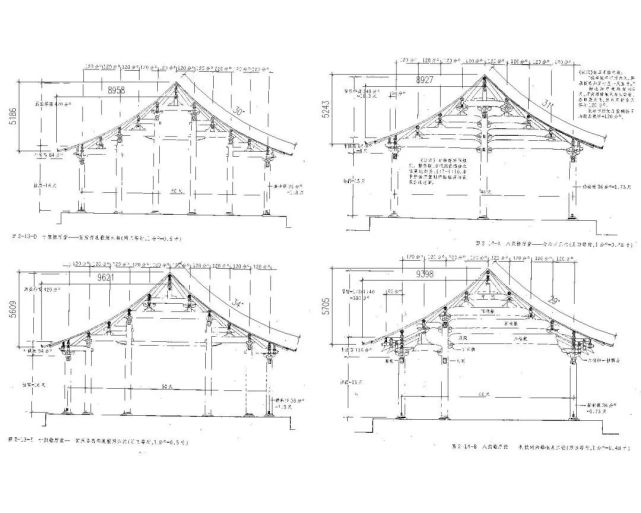
要全面具体地了解宋代建筑与数学的关系，单从画作去了解是不够的，需要结合工程营造的历史资料和现存的古建筑实物进行更深入的剖析。我们主要选取现存宋代建筑代表作——晋祠圣母殿、宋代李诫（一说为李诚）所著的《营造法式》等古建资料作为研究对象。作为整个建筑冠冕的屋面，建筑造型艺术发挥得淋漓尽致。我们的研究着重分析两个数据：屋面的圆心角A（° ）、坡屋面高度半径H/半坡宽度W。

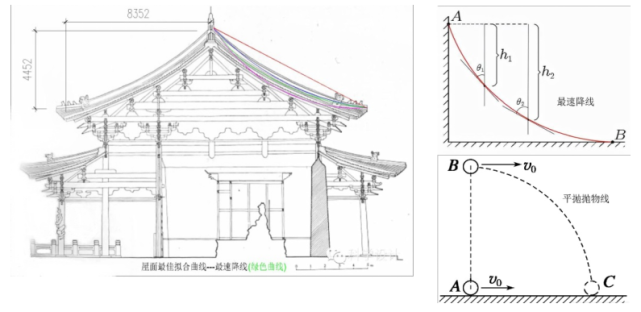
从对屋顶曲线进行数学拟合时，却发现圆弧的拟合度并非最佳。那么什么曲线的拟合度最好？经过对多个屋面曲线的模拟尝试，可以看出绿色的曲线是最佳的。这条曲线是摆线或旋轮线，也叫最速降线
就是在起点与终点确定并且忽略阻力的情形下，物体下滑所需时间最短的曲线。屋面除了审美需求，根本用途是期望能以最快的速度排水
最速降线的理论，是在1696年才由牛顿、伯努利等欧洲的数学家们整明白的，古代的中国工匠们不可能知晓，他们模拟的是圆弧，但是在配合举架的模数确定相关尺寸时，恰好拟合成了最速降线
同时，屋面曲线在檐口处的切线基本水平，使水流排出屋面后，以平抛的抛物线离开屋面，这不得不说又体现了工匠们的智慧
正是这种做法，保证了屋面不积水并且能够把雨水排到最远，以便更好地保护房屋的基础（地盘）
我们以拟合屋面的数学方程的方式，得到最速降线的参数方程：x=R(θ-sinθ), y=R(1-cosθ)。平抛抛物线方程：x²=-2py(p>0, x≥0)
由此我们也得到了一个数学密码：最速降线和平抛抛物线。斗栱与三角不变形原理

古代房屋设计施工一体化，统筹营造者同时也是设计者
比如紫禁城设计师蒯祥，建筑设计世家“样式雷”等等，古代建筑设计者采用了一些与现代建筑设计不同的表达方式。现代建筑设计采用的是绝对尺寸与模数制，图纸上注明绘图比例
而《营造法式》采用的是“材栔分”制，《清式营造则例》采用的是“斗口”制
这两种营造制度，直接以主材尺寸作为绘图基数，其它尺寸均为基数的倍数关系
这样一来，不同规制尺度的建筑，相当于用不同的比例尺对图纸进行放缩，模型或图纸就有了通用性
这是古建筑的第二个数学密码：“材栔分”制和“斗口”制的比例尺作用。
现代制图采用平立剖图、轴测图、透视图绘制，《营造法式》上为了表达清楚层层叠叠的斗栱关系，创造了一种特殊的绘图法：
变角透视图。这是一种介于轴测图和透视图之间的绘图法，
从技术上说，并不符合画法几何的数学投影关系，而是类似于现代广角摄影术。
以此法绘制的图样，兼顾了实用性和可读性，这是一种务实的智慧。这是古建筑的第三个数学密码：变角透视法。